keyg3nme
- Author
-
0x42697262
- Category
-
Linux
- Difficulty
-
Easy
- Play Date
-
2024/11/07 - 2024/11/07
Static Analysis
First checked what type of binary the challenge is.
$ file keyg3nmekeyg3nme: ELF 64-bit LSB pie executable, x86-64, version 1 (SYSV), dynamically linked, interpreter /lib64/ld-linux-x86-64.so.2, BuildID[sha1]=01d8f2eefa63ea2a9dc6f6ceb2be2eac2ca22a67, for GNU/Linux 3.2.0, not stripped
An executable and linkable format 64-bit binary (least signficant bit). Nothing much I can do here. I just know it’s an executable and it runs.
Next I check if there are hardcoded strings.
$ strings keyg3nme/lib64/ld-linux-x86-64.so.2 libc.so.6 __isoc99_scanf puts __stack_chk_fail printf __cxa_finalize __libc_start_main GLIBC_2.7 GLIBC_2.4 GLIBC_2.2.5 _ITM_deregisterTMCloneTable __gmon_start__ _ITM_registerTMCloneTable u/UH []A\A]A^A_ Enter your key: Good job mate, now go keygen me. nope. ;*3$" GCC: (Ubuntu 8.3.0-6ubuntu1) 8.3.0 crtstuff.c deregister_tm_clones __do_global_dtors_aux completed.7963 __do_global_dtors_aux_fini_array_entry frame_dummy __frame_dummy_init_array_entry keyg3nm3.c __FRAME_END__ __init_array_end _DYNAMIC __init_array_start __GNU_EH_FRAME_HDR _GLOBAL_OFFSET_TABLE_ __libc_csu_fini _ITM_deregisterTMCloneTable puts@@GLIBC_2.2.5 _edata __stack_chk_fail@@GLIBC_2.4 printf@@GLIBC_2.2.5 __libc_start_main@@GLIBC_2.2.5 __data_start __gmon_start__ __dso_handle _IO_stdin_used __libc_csu_init __bss_start main __isoc99_scanf@@GLIBC_2.7 __TMC_END__ _ITM_registerTMCloneTable validate_key __cxa_finalize@@GLIBC_2.2.5 .symtab .strtab .shstrtab .interp .note.gnu.build-id .note.ABI-tag .gnu.hash .dynsym .dynstr .gnu.version .gnu.version_r .rela.dyn .rela.plt .init .plt.got .text .fini .rodata .eh_frame_hdr .eh_frame .init_array .fini_array .dynamic .data .bss .comment
Feels like the Good job mate, now go keygen me. and nope are print statements.
I can’t find anything useful other than the main and validate_key.
They look like functions.
Well, main is definitely a function.
$ objdump -d keyg3nme0000000000001165 <main>:
1165: 55 push %rbp
1166: 48 89 e5 mov %rsp,%rbp
1169: 48 83 ec 10 sub $0x10,%rsp
116d: 64 48 8b 04 25 28 00 mov %fs:0x28,%rax
1174: 00 00
1176: 48 89 45 f8 mov %rax,-0x8(%rbp)
117a: 31 c0 xor %eax,%eax
117c: 48 8d 3d 85 0e 00 00 lea 0xe85(%rip),%rdi # 2008 <_IO_stdin_used+0x8>
1183: b8 00 00 00 00 mov $0x0,%eax
1188: e8 c3 fe ff ff call 1050 <printf@plt>
118d: 48 8d 45 f4 lea -0xc(%rbp),%rax
1191: 48 89 c6 mov %rax,%rsi
1194: 48 8d 3d 7f 0e 00 00 lea 0xe7f(%rip),%rdi # 201a <_IO_stdin_used+0x1a>
119b: b8 00 00 00 00 mov $0x0,%eax
11a0: e8 bb fe ff ff call 1060 <__isoc99_scanf@plt> (1)
11a5: 8b 45 f4 mov -0xc(%rbp),%eax
11a8: 89 c7 mov %eax,%edi
11aa: b8 00 00 00 00 mov $0x0,%eax
11af: e8 3a 00 00 00 call 11ee <validate_key> (2)
11b4: 83 f8 01 cmp $0x1,%eax
11b7: 75 0e jne 11c7 <main+0x62>
11b9: 48 8d 3d 60 0e 00 00 lea 0xe60(%rip),%rdi # 2020 <_IO_stdin_used+0x20>
11c0: e8 6b fe ff ff call 1030 <puts@plt>
11c5: eb 0c jmp 11d3 <main+0x6e>
11c7: 48 8d 3d 73 0e 00 00 lea 0xe73(%rip),%rdi # 2041 <_IO_stdin_used+0x41>
11ce: e8 5d fe ff ff call 1030 <puts@plt>
11d3: b8 00 00 00 00 mov $0x0,%eax
11d8: 48 8b 55 f8 mov -0x8(%rbp),%rdx
11dc: 64 48 33 14 25 28 00 xor %fs:0x28,%rdx
11e3: 00 00
11e5: 74 05 je 11ec <main+0x87>
11e7: e8 54 fe ff ff call 1040 <__stack_chk_fail@plt>
11ec: c9 leave
11ed: c3 ret
00000000000011ee <validate_key>:
11ee: 55 push %rbp
11ef: 48 89 e5 mov %rsp,%rbp
11f2: 89 7d fc mov %edi,-0x4(%rbp)
11f5: 8b 4d fc mov -0x4(%rbp),%ecx
11f8: ba ad 0a cb 1a mov $0x1acb0aad,%edx
11fd: 89 c8 mov %ecx,%eax
11ff: f7 ea imul %edx
1201: c1 fa 07 sar $0x7,%edx
1204: 89 c8 mov %ecx,%eax
1206: c1 f8 1f sar $0x1f,%eax
1209: 29 c2 sub %eax,%edx
120b: 89 d0 mov %edx,%eax
120d: 69 c0 c7 04 00 00 imul $0x4c7,%eax,%eax
1213: 29 c1 sub %eax,%ecx
1215: 89 c8 mov %ecx,%eax
1217: 85 c0 test %eax,%eax
1219: 75 07 jne 1222 <validate_key+0x34>
121b: b8 01 00 00 00 mov $0x1,%eax
1220: eb 05 jmp 1227 <validate_key+0x39>
1222: b8 00 00 00 00 mov $0x0,%eax
1227: 5d pop %rbp
1228: c3 ret
1229: 0f 1f 80 00 00 00 00 nopl 0x0(%rax)
| 1 | Takes an input using scanf() |
| 2 | Calls function validate_key. |
I cannot read assembly yet. Thus, I will be using Ghidra for it.
Ghidra
Checking the C code equivalent of the main function, it contains interesting lines.
undefined8 main(void)
{
int iVar1;
long in_FS_OFFSET;
undefined4 local_14;
long local_10;
local_10 = *(long *)(in_FS_OFFSET + 0x28);
printf("Enter your key: "); (1)
__isoc99_scanf(&DAT_0010201a,&local_14); (2)
iVar1 = validate_key(local_14); (3)
if (iVar1 == 1) {
puts("Good job mate, now go keygen me.");
}
else {
puts("nope.");
}
if (local_10 != *(long *)(in_FS_OFFSET + 0x28)) {
/* WARNING: Subroutine does not return */
__stack_chk_fail();
}
return 0;
}| 1 | Asking user input after this print statement |
| 2 | scanf() function |
| 3 | Calls function validate_key |
__isoc99_scanf() is a function that takes two parameters: format and buffer.
This reads a formatted input from the stdin.
See the source code for reference.
local_14 variable is then passed to the validate_key function.
If it’s true, then the input key is valid.
Otherwise, it’s not.
I think that’s basically how the main flow of this program works.
The C-equivalent of the assembly code for validate_key is quite simple.
bool validate_key(int param_1)
{
return param_1 % 0x4c7 == 0;
}|
Note that 0x4c7 is base-16 (hexadecimal). Converting this to base-10 (decimal), it is equivalent to 1223. |
The algorithm at the core validates the input integer by testing its divisibility by the constant 0x4c7, equivalent to 1223.
The program applies a modulus operation to the input:
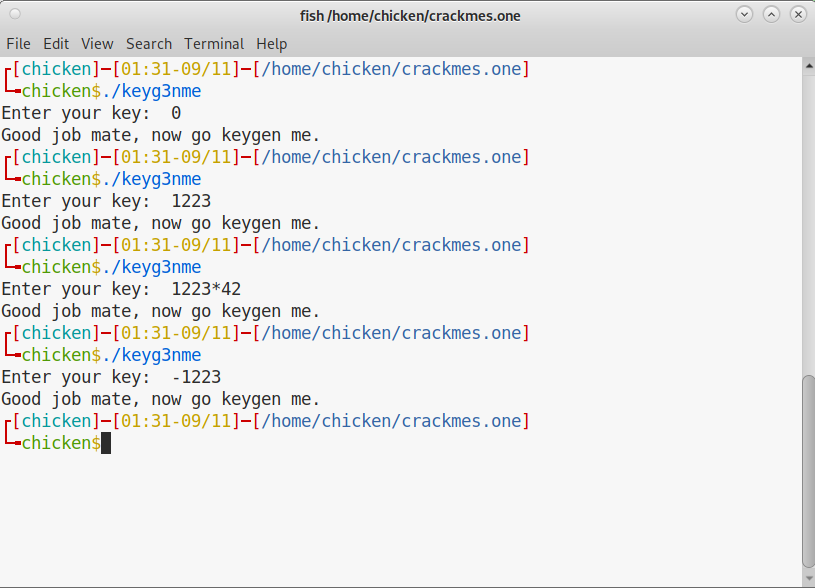
If the result of this operation is zero, the input parameter integer is considered valid. Thus, only multiples of 1223 pass the verification step.
Dynamic Analysis
There’s no dynamic analysis needed ;)
Actually, I only tested some inputs randomly. All of them failed to verify of course.
However, we already know the algorithm of the keys. Simply input an integer that is divisible by 1223.
Keygen
Time to create a key generator! I am using Python for this one. It’s possible to create it with bash but I prefer this language more.
import random
key = 1223 * random.randint(0, 1223)
print(f"Generated Key: {key}")Consider this challenge solved!
Conclusion
This challenge wasn’t that difficult to solve. I expected that the algorithm were to be more complicated. I was surprised it was that easy. This might ihdicate that harder challenges might have different methods of algorithms but with the same concept.
There is a caveat on this challenge though. Even if the key were to be valid, it does not accept them.
For example, if the input key were to be 1223*3234567, it’s accepted.
But when the actual value is used as input: 3955875441, this fails as a valid key.
When I test 3234567*1223, the verification fails.
Meaning, the code only checks 1223 and ignores the rest.
I don’t know how it works but that’s how it works.
I am guessing that the reason why it fails to validate big numbers is because it overflows the datatype int.